Encoder
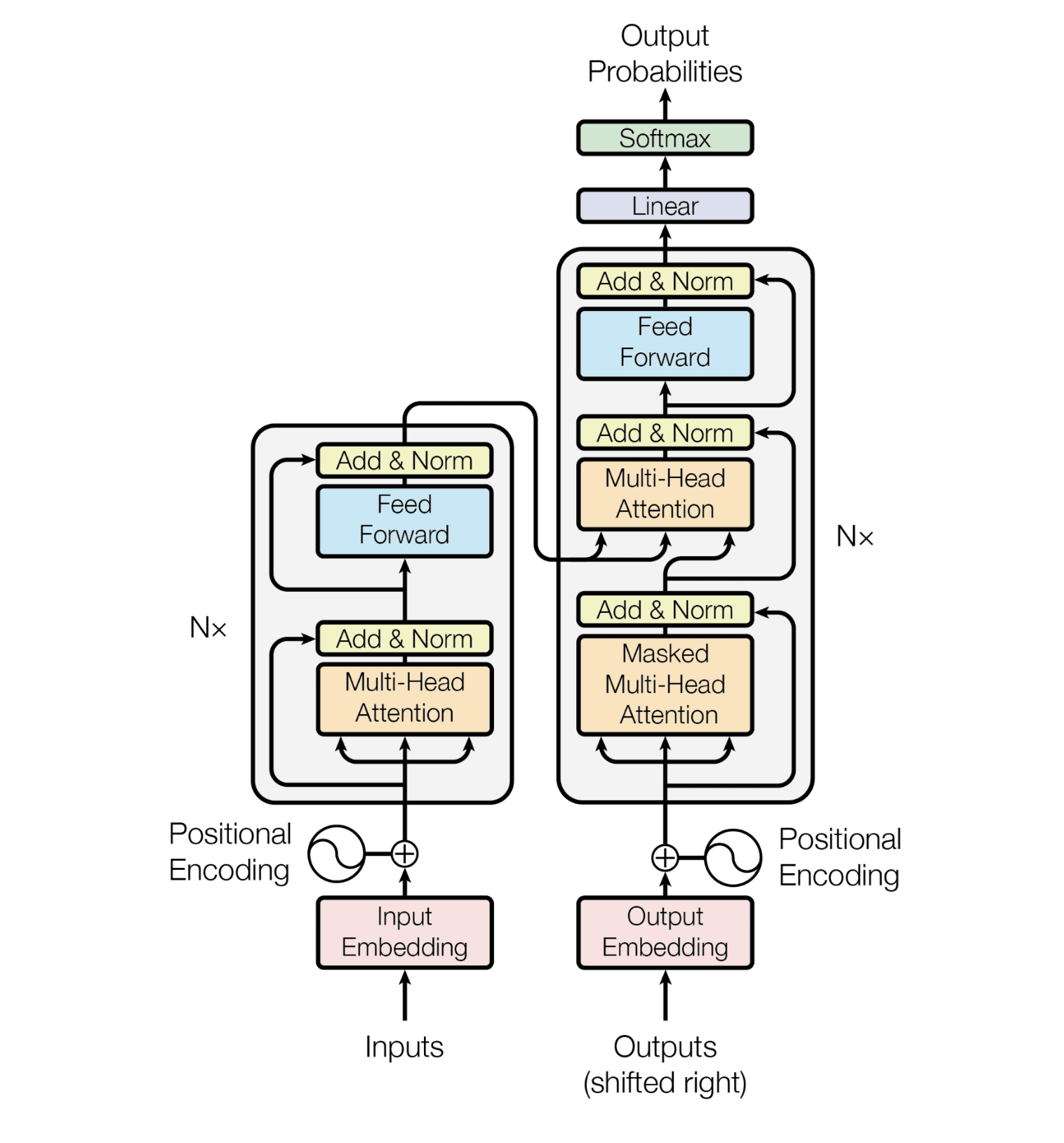
this is a blog about the encoder in transformer
Token Embedding
class TokenEmbedding(nn.Embedding):
def __init__(self, vocab_size, d_model):
super(TokenEmbedding, self).__init__(vocab_size, d_model, padding_idx=1)
Position Embedding
Position embedding is essential, and its mathematical formula is well worth your time. With position embedding, we can input a sentence of different lengths and use the same embedding math formula to embed its position information.
Let \(t\) be the desired position in an input sentence, \(\vec{p}_t \in \mathbb{R}^d\) be its corresponding encoding, and \(d\) be the encoding dimension (where \(d \geq 0\)). Then \(f : \mathbb{N} \rightarrow \mathbb{R}^d\) will be the function that produces the output vector \(\vec{p}_t\) and it is defined as follows:
\[\vec{p}_t^{(i)} = f(t)^{(i)} := \begin{cases} \sin(\omega_i \cdot t), & \text{if } i = 2k \\ \cos(\omega_i \cdot t), & \text{if } i = 2k + 1 \end{cases}\]where
\[\omega_i = \frac{1}{10000^{2i/d}}\]class PositionalEmbedding(nn.Module):
def __init__(self, d_model, maxlen, device):
super(PositionalEmbedding, self).__init__()
self.encoding = torch.zeros(maxlen, d_model, device=device) # initialize the encoding
self.encoding.requires_grad_(False) # This encoding does not require a gradient
# generate the position (The most important one in positional embedding!!!):
pos = torch.arange(0, maxlen, device=device) # generate a series from 0 to maxlen-1 [0, 1, ... , maxlen-1]
pos = pos.float().unsqueeze(1) # add a dimension [[0.], [1.], ... , [maxlen-1]]
_2i = torch.arange(0, d_model, 2, device=device) # generate 2i: [0, 2, 4, ...]
self.encoding[:, 0::2] = torch.sin(pos / (10000 ** (_2i / d_model)))
self.encoding[:, 1::2] = torch.cos(pos / (10000 ** (_2i / d_model)))
def forward(self, x):
# there is no need to RETURN all the arguments, so make a cut with seq_len
seq_len = x.shape[1]
return self.encoding[:seq_len, :]
Layer Norm
Why do we need normalization
In deep neural networks, the layers will directly or indirectly affect each other; a slight change in one layer may lead to different layers of violent shock, resulting in the corresponding network layer falling into saturation and model training difficulties. This phenomenon is called “Internal Covariate Shift.” [For example, in the sigma function, when \(x>10\), the gradient value is close to 0, and the gradient of the lower neural network disappears in the BP process].
In order to reduce this effect, so it is handled in terms of intuitive data distribution by normalizing the batch data to an \(N(0,1)\) distribution, which allows for a manageable range of input data distributions for each layer.
Two normalization methods are often used in deep neural networks: batch normalization and layer normalization.
Batch normalization is generally used in the CV domain, while layer normalization is generally used in the NLP domain.
The equations of these two normalization methods are formally the same:
\(N(x) = \gamma \left(\frac{x - \mu(x)}{\sigma(x)}\right) + \beta\) where \(\gamma\) and \(\beta\) are affine parameters learned from data, \(\mu (x)\) and \(\sigma (x)\) are the mean and standard deviation. Batch normalization computes \(\mu (x)\) and \(\sigma (x)\) across batch size and spatial dimensions independently for each feature channel. However, layer normalization computes \(\mu (x)\) and \(\sigma (x)\) across all channels for each sample.
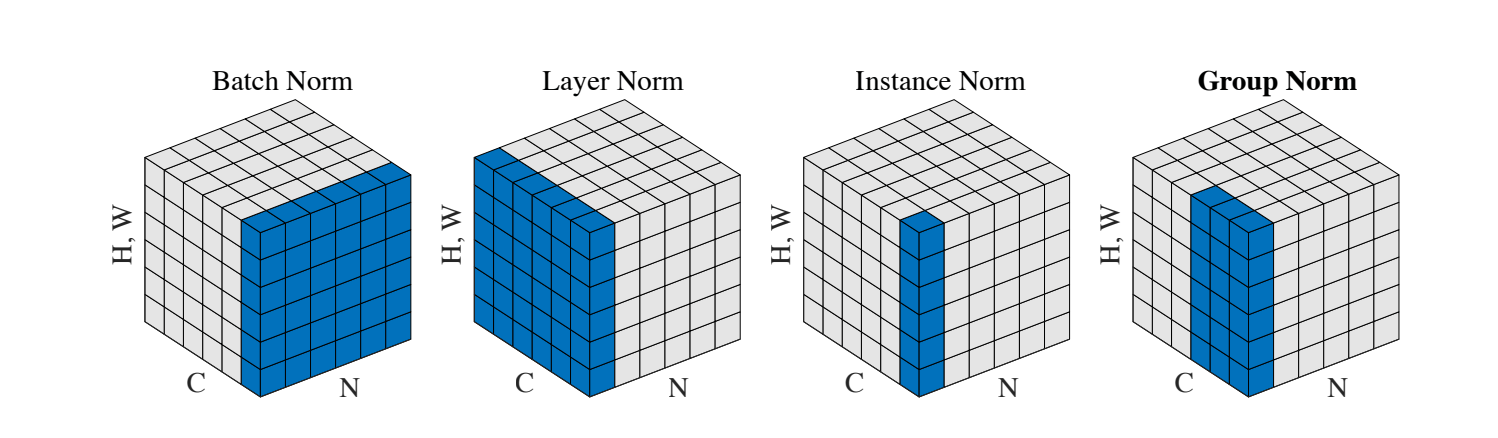
As in NLP the above figure of C, N, H,W:
- N: N sentences, i.e. batchsize;
- C: length of a sentence, i.e. seqlen;
- H,W: word vector dimension embedding dim.
class LayerNorm(nn.Module):
def __init__(self, d_model, eps=1e-10):
super(LayerNorm, self).__init__()
self.gamma = nn.Parameter(torch.ones(d_model))
self.beta = nn.Parameter(torch.zeros(d_model))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
var = x.var(-1, unbiased=False, keepdim=True)
out = (x - mean) / torch.sqrt(var + self.eps)
out = self.gamma * out + self.beta # Finally, the result is scaled and offset.
return out
FFN
FFN is essentially a two-layer MLP. The mathematical equation of this MLP is:
\[FFN(x) = \max (0, x \cdot W_1 + b_1) \cdot W_2 + b_2\]FFN can increase the expressive power of a model by adding a nonlinear transformation between two FCs, allowing the model to capture complex features and patterns.
class PositionwiseFeedForward(nn.Module):
def __init__(self, d_model, hidden, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.fc1 = nn.Linear(d_model, hidden)
self.fc2 = nn.Linear(hidden, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
x = self.fc1(x)
x = F.relu(x)
x = self.dropout(x)
x = self.fc2(x)
return x
Transformer Embedding
The Token Embedding module and Positional Embedding module are put together to form the Transformer Embedding module.
class TransformerEmbedding(nn.Module):
def __init__(self, vocab_size, d_model, max_len, drop_prob, device):
super(TransformerEmbedding, self).__init__()
self.tok_emb = TokenEmbedding(vocab_size, d_model)
self.pos_emb = PositionalEmbedding(d_model, max_len, device)
self.drop_out = nn.Dropout(p=drop_prob)
def forward(self, x):
tok_emb = self.tok_emb(x)
pos_emb = self.pos_emb(x)
return self.drop_out(tok_emb + pos_emb)
Multi-Head Attention
The detail about Multi-Head Attention can be found in here.
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, n_head):
super(MultiHeadAttention, self).__init__()
self.n_head = n_head
self.d_model = d_model
self.w_q = nn.Linear(d_model, d_model)
self.w_k = nn.Linear(d_model, d_model)
self.w_v = nn.Linear(d_model, d_model)
self.w_combine = nn.Linear(d_model, d_model)
self.softmax = nn.Softmax(dim=-1)
def forward(self, q, k, v, mask=None):
batch, time, dimension = q.shape
n_d = self.d_model // self.n_head
q, k, v = self.w_q(q), self.w_k(k), self.w_v(v)
q = q.view(batch, time, self.n_head, n_d).permute(0, 2, 1, 3)
k = k.view(batch, time, self.n_head, n_d).permute(0, 2, 1, 3)
v = v.view(batch, time, self.n_head, n_d).permute(0, 2, 1, 3)
score = q @ k.transpose(2, 3) / math.sqrt(n_d)
if mask is not None:
# mask = torch.tril(torch.ones(time, time, dtype=bool))
score = score.masked_fill(mask == 0, -1e9)
score = self.softmax(score) @ v
score = score.permute(0, 2, 1, 3).contiguous().view(batch, time, dimension)
output = self.w_combine(score)
return outpu
Encoder Layer
Putting all the parts together makes up the Encoder part of the Transformer.
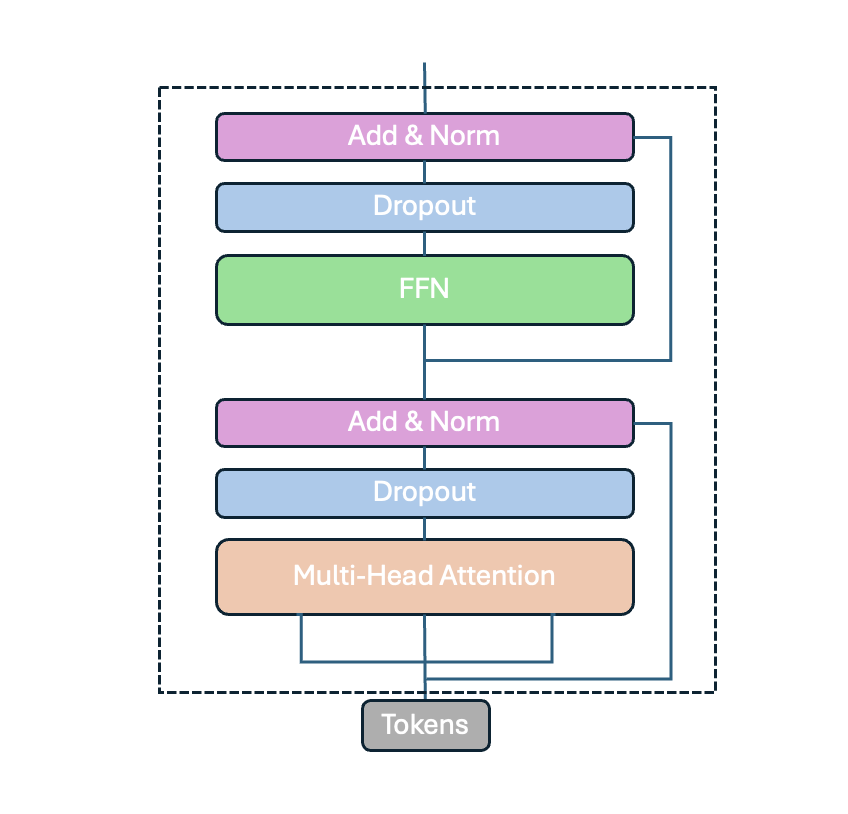
class EncoderLayer(nn.Module):
def __init__(self, d_model, ffn_hidden, n_head, drop_prob) -> None:
super(EncoderLayer, self).__init__()
self.attention = MultiHeadAttention(d_model, n_head)
self.norm1 = LayerNorm(d_model)
self.drop1 = nn.Dropout(drop_prob)
self.ffn = PositionwiseFeedForward(d_model, ffn_hidden, drop_prob)
self.norm2 = LayerNorm(d_model)
self.drop2 = nn.Dropout(drop_prob)
def forward(self, x, mask=None):
_x = x
x = self.attention(x, x, x, mask)
x = self.drop1(x)
x = self.norm1(x + _x)
_x = x
x = self.ffn(x)
x = self.drop2(x)
x = self.norm2(x + _x)
return x